近日，《物理评论快报》（Physical Review Letters, PRL）发表题为Proposed Model of the Giant Thermal Hall Effect in Two-Dimensional Superconductors: An Extension to the Superconducting Fluctuations Regime的研究论文。西湖大学物理讲席教授Alexey Kavokin为第一作者和通讯作者。
A research article named Proposed Model of the Giant Thermal Hall Effect in Two-Dimensional Superconductors: An Extension to the Superconducting Fluctuations Regime appeared recently in Physical Review Letters (PRL). Alexey Kavokin, Chair Professor of Physics of Westlake University, is the first author and the correspondent author.
《自然》期刊2019年报道，人们在铜氧化物高温超导体中发现了巨大的热霍尔效应，引发很多后续实验与讨论。Kavokin教授和合作者研究处于超导临界温度以上的二维超导材料，为霍尔热导率随着温度迅速增加等一系列实验现象提供了统一解释。
As reported in Nature, 2019[1]，a giant thermal Hall effect is observed in several pseudogap cuprates. The origin and interpretation of this effect remained obscure. It triggered a number of follow up experiments and discussions. Kavokin and collaborators studied the thermal Hall effect in two-dimensional superconductors above the critical temperature, offering a unified approach to the interpretation of the observed phenomena, such as the superlinear increase of thermal Hall conductivity with the decrease of temperature, in a large variety of experimentally studied systems.
热霍尔效应这么大，究竟是怎么了？
The thermal Hall effect is huge, and why is it?
热霍尔效应是在温度梯度和磁场的共同作用下形成热流。一个导体上在x轴方向存在温度梯度
在垂直于温度梯度的z轴方向外加一个磁场H，则在y轴方向形成热流q（见图1）。如果以我们更为熟悉的霍尔效应做类比，霍尔效应里的电场可类比热霍尔效应里的温度梯度，而电流可类比热流。和霍尔效应一样，热霍尔效应的存在，表明体系破坏了时间反演对称性和镜面反射对称性。通常在金属中，霍尔热效应非常弱，满足维德曼–夫兰兹定律（Wiedemann-Franz law）。
The thermal Hall effect consists of a generation of a heat flow by a combined action of the temperature gradient and magnetic field. As shown in Figure 1, a heat flow q is generated in the direction that is perpendicular both to the magnetic field H and the temperature gradient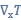
applied. If we draw an analogy between the Hall effect and the thermal Hall effect, the electrical field in the former corresponds to the temperature gradient in the latter, and the electrical current in the former corresponds to the heat flow in the latter. The thermal Hall effect, in a remarkable similarity to the electronic Hall effect, proves that the time-reversal symmetry and the mirror reflection symmetry of the system are broken. As follows from the Wiedemann-Franz law, the thermal Hall effect in metals is usually very weak.
图1 热霍尔效应示意图。在x方向的温度梯度
和z方向的磁场H的共同作用下，产生y方向的热
流。
Figure 1. The schematic showing the thermal Hall effect. The thermal flow q in the y direction is a combined action of the temperature gradient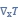 
in the x direction and magnetic field H in the z direction.
然而2019年有实验表明，在La1.6−xNd0.4SrxCuO4, La1.8−xEu0.2SrxCuO4, La2−xSrxCuO4 ，Bi2Sr2−xLaxCuO6+δ，这些高温超导铜氧化合物的赝能隙态中霍尔热导κyx 的绝对值比在我们熟悉的金属中整整大了两个数量级，且呈负值，严重偏离维德曼–夫兰兹定律。
Nevertheless, a giant increase of the thermal Hall conductivity κyx violating the Wiedemann-Franz law has been reported since 2019 in several pseudogap cuprates such as La1.6−xNd0.4SrxCuO4, La1.8−xEu0.2SrxCuO4, La2−xSrxCuO4 ，Bi2Sr2−xLaxCuO6+δ . The absolute value of κyx is larger than one anticipated for conventional metals by about 2 orders of magnitude, and κyx has a negative sign, surprisingly.
对于这些材料的霍尔热导所呈现的共同特征（负值、随温度超线性下降），人们做了很多后续实验并尝试提出了多种解释，但这些解释基本只针对某个系统，还没有理论可以做出统一解释。Kavokin和合作者试图建立一个简单模型，揭示这些实验观察背后共同的机制。
There have been a number of following experiments and attempts to the interpretation of the observed effects. The thermal Hall conductivity demonstrated the same feature (negative sign and the superlinear increase with the decrease of temperature) in a number of very different systems ranging from fluctuation superconductors above the critical temperature to the disordered normal metals. A multitude of possible reasons of the effect had been proposed for each studied system, while no unified approach to the interpretation was available. Kavokin and collaborators formulate a simple model that reveals the common mechanism behind these observations.
建立简单模型，揭示共同机制
A simple model, the common mechanism
通过分析铜氧化物赝能隙态的实验数据，Kavokin和合作者认为，霍尔热导这么大是由两个因素造成的。一是由于其磁化强度随温度的变化率在温度降低时急速增加，在接近相变处尤甚；二是由于化学势的随温度的变化率也是非常大，相比在无相互作用的简并费米气中要大得多。
Analyzing the recent experimental data on pseudogap cuprates, Kavokin and collaborators concluded that the giant thermal Hall conductivity found in these systems might take place due to the combination of 2 factors. First, the temperature derivative of the magnetization shows a strong increase with the decrease of temperature, especially in the vicinity of the superconducting phase transition. Second, the temperature derivative of the chemical potential does not contain the smallness characteristic of the noninteracting degenerate Fermi gas in all studied materials.
Kavokin和合作者从热动力学入手，将κyx和系统的热力学系统平衡态相联系。他们以一个稳定的（具有恒定化学势）的开路（无电流经过）为研究系统，利用涨落理论（fluctuation theory），推导出一般金属和超导体的霍尔热导κyx 的解析表达式。
Kavokin and collaborators developed a general thermodynamic approach that links
κyx to the equilibrium characteristics of the systems under study. They consider an open circuit geometry (no electric current) in the stationary regime (characterized by the constant electrochemical potential). In the framework of the fluctuation theory, they derived the analytical expressions for κyx both for superconductors in various regimes and for a normal metal.
在这个模型里，热霍尔效应是由化学势的随温度变化率（dμ/dT）和系统磁化的随温度变化率（dM/dT）决定的。因此，霍尔热导κyx可以用两者的乘积来表示：
.
而铜氧化物呈现那么大的热霍尔效应，正是蕴含在这一简单的关系中。
In this model, the thermal Hall conductivity is governed by the product of the chemical potential derivative over temperature(dμ/dT ) and the magnetization derivative over temperature (dM/dT ).
.
This simple relation sheds light on the physics that is behind the recently observed giant thermal Hall effect in cuprates.
Kavokin和合作者仔细研究了两种情况对热霍尔效应的影响。第一种情况是超导体中库珀对的涨落（接近超导临界温度
和高温极限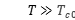
下）。第二种情况是普通金属中的电子相互作用，虽然此时电子不会形成库珀对，但电子的相互排斥带来有效质量的重正化，而这一重正化和温度相关。
Kavokin and collaborators carefully investigated two factors that play important roles in the thermal Hall effects. First, the fluctuating Cooper pairs that exist above the superconducting phase transition (close to the critical temperature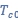 
and in the high temperature limit 
). Second, the repulsive interaction in normal metals that may be considered as a counterpart of Cooper pairing and that leads to the renormalization of the electron effective mass.
这两种情况下，霍尔热导的随温度变化率要比无相互作用电子气中的大得多，这也就解释了霍尔热导的超线性增长
In both cases, the temperature derivative of the thermal Hall conductivity is much larger than one of a degenerate Fermi gas of noninteracting electrons. This qualitatively explains the observed giant thermal Hall effect.
此外，Kavokin和合作者还研究了在量子涨落区域（domain of quantum fluctuations）的霍尔热导，发现热导率呈负值，且绝对值随温度降低而急速增加。
Kavokin and collaborators investigated further the behavior of thermal Hall conductivity in the domain of quantum fluctuations. They found that it always has a negative sign, and its absolute value increases rapidly with the temperature decrease.
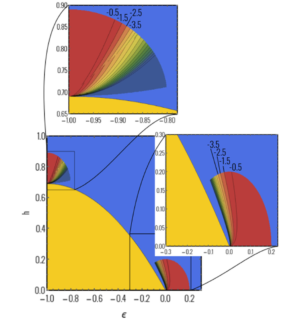
图2 霍尔热导与无量纲温度ε及磁场h之间的关系。有效范围为临界温度附近以及第二临界场附近（图中的蓝色区域代表普通相，黄色表示超导态）。
Figure 2. Fluctuation induced thermal Hall conductivity as a function of dimensionless temperature ε and magnetic field h . Our consideration is valid in the blue area in the domain close to the critical temperature and in the vicinity of the second critical filed(The blue area shows the normal phase above superconducting transition, the yellow area corresponds to the superconducting state).
Kavokin和合作者的理论基于一个相当简单的模型，但却能够解释此前的实验结果中霍尔热导为什么呈负值，且绝对值随着温度降低而增加。这项工作对理解强关联物理体系中的热输运性质，特别是它和高温超导系统涨落效应的关系，有重要意义。
Based on this simple model, Kavokin and collaborators explained the experimentally observed negative sign of the thermal Hall conductivity and the increase of its absolute value with the decrease of temperature. This work is important for the physics community as it helped us better understand the thermal transfer properties in strongly correlated systems, and especially their relation to the fluctuation effects in high-temperature superconducting systems.
