Physics of Quantum Computation

Boris Altshuler

Professor

Columbia University, New York

Speaker

主讲嘉宾

Boris Leonidovich Altshuler is a professor of physics at Columbia University. His specialty is theoretical condensed matter physics.

Altshuler received his diploma in physics from Leningrad State University in 1976. He continued on at the Leningrad Institute for Nuclear Physics, where he was awarded his Ph.D. in physics in 1979. Altshuler stayed at the institute for the next ten years as a research fellow.

In 1989, Altshuler joined the faculty of the Massachusetts Institute of Technology. While there, he received the Hewlett-Packard Europhysics Prize (now called the Agilent Physics Prize) and became a fellow of the American Physical Society.

Altshuler left MIT in 1996 to take a professorship at Princeton University. While there, he became affiliated with NEC Laboratories America. Recently, Altshuler has joined the faculty of Columbia and continues to work with the NEC Labs.

Abstract

讲座摘要

Development of devices for quantum computation is now extremely popular field, which is generously supported by both industry and government agencies and enjoys tremendous progress. However a clear understanding of advantages of the quantum information processing as compared to classical ones is far from being achieved.

A classical computer consists of a large number N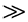1 of bits – systems that have two possible states, e.g. 0 and 1. Each state of a classical computer is fully characterized by the states of all its bits – a sequence of numbers 0 and 1 usually called a bit-string. The number of the possible bit-strings,  2^N can be enormously big. The most interesting for the practical applications are optimization problems, which can be reduced to a search for a minimum of some particular function of bit-strings. It is likely although not proven that classical computer needs exponentially long time to solve such problems. The most desirable would be to develop a quantum computer able to accelerate solution of optimization problems as compared to the best classical algorithms.

Quantum mechanics makes it possible to create states, which are linear combinations of different bit-strings. Accordingly the amount of information contained in a given quantum state increases exponentially with N. In order to understand how to control the quantum states of a system of qubits one can use methods developed in the physics of many-body systems, in particular, the theory of Many-Body Anderson Localization.

The talk will be devoted to discussion of such analysis and its possible quantum algorithms that it suggests.